Андрей Соломонович Бершадский
д-р Физ.-Мат наук.
Что нужно для того, чтобы проверить число на простоту? Лучше всего попробовать его факторизовать. Если будет обнаружен хоть один делитель, то число не является простым. Но, здесь несколько проблем, средь которых величина числа и его сомножителей. Если большое нечетное число делится всего на два почти одинаковых по величине простых сомножителя, то факторизация затянется на астрономическое количество времени и дождаться ее окончания практически невозможно.
Поэтому для проверки простоты чисел необходимо воспользоваться другими методами, средь которых такие, как: метод Миллера - Рабина и метод Лукаса - Лемера. За одним исключением - оба они являются вероятностными и никакой гарантии простоты не обещают. Хотя можно вычислить вероятность того, что число, прошедшее через эти методы проверку и названное не составным, является простым. Иначе говоря, существует бесконечное количество чисел именуемых кармайкловыми, которые ведут себя точно также, как и простые, согласно малой теореме Ферма и имеют абсолютно одинаковые свойства. Благодаря чему саму Малую теорему следует немного уточнить, начиная со слов: "Если число простое или кармайклово ...", а далее по тексту.
Избежать данных недоразумений можно с помощью дополнительных методов, средь которых, например, числится N-1. Число N прошедшее проверку с помощью методов Миллера - Рабина и Лукаса - Лемера, в дальнейшем подвергается дополнительной проверке. Для этого берут число на единицу меньшее N-1 и подвергают факторизации. Причем, N-1 в большинстве случаев разложить на делители намного проще, нежели N из двух больших сомножителей. Например, можно сразу сказать, что одним из сомножителей будет обязательно 2. В результате получаем:
N-1 = П q(i);
где:
q(i) - некоторый простой сомножитель числа N-1, а i - количество таких сомножителей.
После чего, останется лишь взять все q и для каждого из них провести дополнительную проверку, на предмет того имеется ли общий делитель у чисел (a^((N - 1) / q(i))) - 1 и N. В качестве a можно брать любое число большее 1 и меньшее N. Кратность выясняется с помощью алгоритма наибольшего общего делителя Евклида (НОД). Для каждого из простых сомножителей числа N-1 такую проверку достаточно провести единожды. Проще говоря, если хоть какое кратное будет найдено, то оно и является тем самым делителем числа N, а следовательно N не является простым.
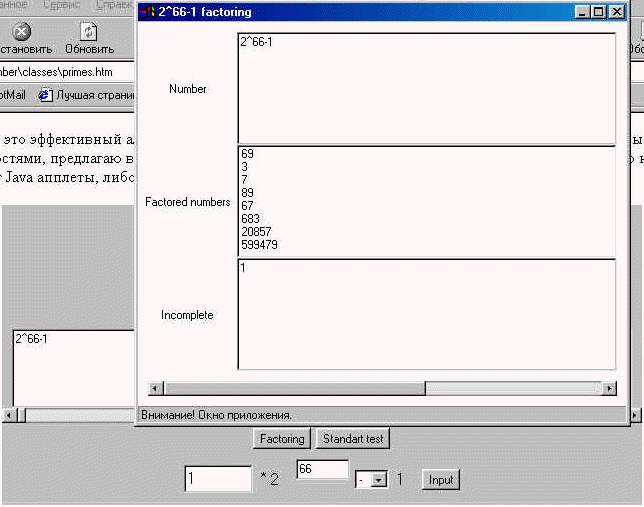
Единственная тонкость - это эффективный алгоритм факторизации, с помощью которого можно разложить N-1. Чтобы не мучиться с алгоритмическими тонкостями, предлагаю воспользоваться нижеприведенным апплетом для этой цели, любезно предоставленным для примера данной лекции Юрием Решетовым. (Если вы его не видите, то значит ваш браузер не поддерживает Java апплеты, либо их поддержка выключена).
Для того, чтобы проверить или факторизовать число, его нужно ввести в многострочное текстовое поле, где по умолчанию находятся девятнадцать единиц (кстати, число простое). Для факторизации надо воспользоваться кнопкой "Factoring", а для проверки на простоту методами Миллера - Рабина и Лукаса - Лемера, кнопкой "Standart Test". Нижняя часть позволяет задать число в виде a*2^b(+/-)1, т.е. в компактном представлении, которое можно вывести в верхнее окошко с помощью кнопки "Input".
Например, попробуем разложить на сомножители число 2^67-1. Тесты сразу же покажут, что оно является составным. Впрочем, доверять тестам я бы не советовал. Поэкспериментируйте, например, с такими числами, как 7 и 15. И вы убедитесь, что иногда стандартные тесты сообщают что 7 является составным, а 15 простым, хотя это не так. Чтобы не попасть впросак, надо выудить с помощью факторизации хотябы один сомножитель. У нашего числа 2^67-1 их два и оба крупные. Факторизация в лоб займет значительное время. Гораздо проще воспользоваться методом N-1. Поскольку 2^67-2 = 2*(2^66-1), то и разложим число 2^66-1. Несколько секунд на Athlon 1700XP+ и мы видим результат:

Осталось только:
взять произвольное число a
возвести его в степень (2^66-1)/599479
из результата вычесть 1
и с помощью алгоритма наибольшего общего делителя с результатом и числом 2^67-1, получить один из сомножителей: 193707721 или 761838257287.
Если бы исследуемое число было простым, то получить делители вышеприведенным методом для нашего числа так и не удалось бы - их не должно существовать.
Литература
Акритас А. Основы компьютерной алгебры с приложениями. М.: Мир, 1994.
Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черёмушкин А.В. Основы криптографии. М.: Гелиос АРВ, 2002. 2-е изд.
Анохин М.И., Варновский Н.П., Сидельников В.М., Ященко В.В. Криптография в банковском деле. М.: МИФИ, 1997.
Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979.
Березин И.С., Жидков Н.П. Методы вычислений. Т. 1. М.: Наука, 1966.
Берлекэмп Э. Алгебраическая теория кодирования. М.: Мир,1971.
БоревичЗ .И., ШафаревичИ . Р. Теория чисел. М.: Наука, 1985.
Ван дер Варден Б.Л. Алгебра. М.: Наука, 1976.
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. — М.: МЦНМО, 2003.—328 с.
Василенко О.Н. Современные способы проверки простоты чисел. Обзор // Кибернетич. сборн. 1988. Вып. 25. С. 162—188.
Василенко О.Н. Некоторые алгоритмы построения больших простых чисел // Вестн. Моск. ун-та. Сер. 1. Матем. Механ. 1997. №5. С. 62—64.
Василенко О.Н. О некоторых свойствах чисел Ферма // Вестн. Моск. ун-та. Сер. 1. Матем. Механ. 1998. №5. С. 56—58.
Василенко О.Н. Об алгоритме Миллера—Рабина // Вестн. Моск. ун-та. Сер. 1. Матем. Механ. 2000. №2. С. 41—42.
Виноградов И.М. Основы теории чисел. М.: Наука, 1972.
Гашков С. Б. Упрощенное обоснование вероятностного теста Миллера-Рабина для проверки простоты чисел // Дискретная математика. 1998. Т. 10 (4). С. 35—38.
Дэвенпорт Дж., Сирэ И., Турнье Э. Компьютерная алгебра. М.:Мир, 1991.
Карацуба А.А., Офман Ю.П. Умножение многозначных чисел на автоматах // ДАН СССР. 1961. Т. 145 (2). С. 293—294.
Касселс Дж. Введение в геометрию чисел. М.: Мир, 1965.
Кнут Д. Искусство программирования. Т. 2. Получисленные алгоритмы. Вильямс: М.—СПб.—Киев, 2000. 3-е изда ние.
Кострикин А.И. Введение в алгебру. М.: Наука, 1977.
Лемеш А.Н. О низких числах // Тезисы докл. 12 междунар. конф. «Проблемы теоретической кибернетики». Часть II. Ниж. Новг., 1999. С. 135.
Ленг С. Введение в теорию диофантовых приближений. М.: Мир, 1970.
(2). С. 91—101.
Нечаев В.И. Элементы криптографии. М.: Высшая школа, 1999.
Ноден П., Китте К. Алгебраическая алгоритмика. М.: Мир, 1999.
Панкратьев Е.В. Компьютерная алгебра. Факторизация многочленов. М.: Изд-во МГУ, 1988.
Уильямс Х. Проверка чисел на простоту с помощью вычислительных машин // Кибернетич. сборн. 1986. Вып. 23. С. 51—99.
Чебышев П.Л. Полное собрание сочинений. Т. 1. Теория чисел. Изд-во АН СССР, 1946.
Чистов А.Л. Алгоритм полиномиальной сложности для разложения многочленов и нахождения компонент многообразия в субэкспоненциальное время // Зап. науч. семин. ЛОМИ АН СССР. 1984. №137. С. 124—188.